注意 该博客是为了帮助同学学习,并非为了协助同学刷题,请读者保持自觉,请勿做CV工具人 。另外为了节省篇幅,代码中不再写明#include,如果遇到我没有声明的函数,那么就是某一个头文件中的函数,读者搜索“c + 函数名字”就能查到相关信息。
小A遇到了一座神奇的泉水,在泉水中洗涤会大幅增加他的精力。在一次洗涤中,泉水增加力量的数值为当前力量二进制表示中的最低位的1对应的值。
例如:
如果当前力量为9(1001 最低位1对应的值为1),增加的力量为1;
如果当前力量为12(1100 最低位1对应的值为100),增加的力量为4。
小A想要将他的力量变为2的幂次数,他需要在泉水中洗涤多少次呢?
输入格式 多样例测试。
第一行输入T(T <= 100,000),代表样例数;
剩余T行,每行输入一个数n(n < 1,000,000,000)代表小A当前的力量。
输出格式 对于每次询问,输出小A需要在泉水中洗涤的次数。
输入样例 4
输出样例 0
题解 多写了的内容 这道题涉及到2的整数次幂的运算,我们科普一个知识点,就是2的整数次幂的特点。仔细观察2的整数次幂可以发现,每一个2的整数次幂的二进制表达式都只有一个1。
比如:1的二进制表达是0b1,2的二进制表达是0b10,4的二进制表达是0b100,以此类推。
所以我们也可以得到一种O(1)复杂度计算2的整数次幂的方法:2n = 1 << n。
这道题需要判断是否是2的整数次幂,我们可以把int范围内的所有值都列出来(打表打表,都可以打表
这里我们写一个函数(int check(int n, int start))来判断一个数是否为2的整数次幂。其中n是要进行判断的数,start是从表中哪个位置开始搜索,返回值是返回返回下一次从哪个地方开始搜索,返回-1表示当前值已经是2的整数次幂了,返回-2表明计算错误。start的存在意义是减小搜索范围,通过观察我们不难发现,每次运算过后值只会变大不会变小,所以当前搜索过的地方下一次在这里也不会搜索到结果。
中间的k为什么只初始化了一次也单独强调一下,观察计算过程可以发现,k每次只会变大不会变小,所以我们每次运算从上一次结束的地方开始就可以了,不需要从头开始,也可以节省运算资源。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 int t[ ] = { 1 , 2 , 4 , 8 , 16 , 32 , 64 , 128 , 256 , 512 , 1024 , 2048 , 4096 , 8192 , 16384 , 32768 , 65536 , 131072 , 262144 , 524288 , 1048576 , 2097152 , 4194304 , 8388608 , 16777216 , 33554432 , 67108864 , 134217728 , 268435456 , 536870912 , 1073741824 } ; int check ( int n, int start) { for ( int i = start; i != 31 ; ++ i) { if ( t[ i] == n) return - 1 ; else if ( t[ i] > n) return i; } return - 2 ; } int main ( ) { int a; scanf ( "%d" , & a) ; = false; while ( a-- ) { if ( start) printf ( "\n" ) ; else start = true; int n; int i = 0 ; int k = 1 ; scanf ( "%d" , & n) ; int result = 0 ; int preStart = 0 ; while ( ( preStart = check ( n, preStart) ) != - 1 ) { ++ result; for ( ; i != 30 ; ++ i) { if ( ( ( n >> i) & 1 ) == 1 ) break ; <<= 1 ; } += k; } printf ( "%d" , result) ; } return 0 ; }
该解法的代码由群友——ty提供:
其中lowbit的原理见:lowbit的原理及证明
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 int lowbit ( int x) { return x & ( - x) ; } int main ( ) { int n; scanf ( "%d" , & n) ; int i; while ( n-- ) { int x; scanf ( "%d" , & x) ; int t = 0 ; while ( true) { if ( x == lowbit ( x) ) break ; = x + lowbit ( x) ; ++ ; } printf ( "%d\n" , t) ; } return 0 ; }
小 A 踏上了 AK 这场新生赛的旅程。但对方太狡猾,将小 A 传送到了一个不知名的地方。经过探查,小 A 发现了一座很大的迷宫。这座迷宫从上方看竟然是正方形的,而且内部被分为了 1000∗1000 个同等大小房间,而狡猾的敌人则隐藏在某些房间中,准备偷袭小 A.
幸好小 A 提前发现了对方的阴谋,准备解决所有的敌人。但敌人太多了,小 A 准备使用高级魔法—“这题我会”。这个魔法的作用范围是正好是一个矩形,能够覆盖W∗H个房间(注意:W∗H与H∗W是不同的,如:2∗3 与 3∗2 是两种魔法),处于该范围内的敌人将会被魔法消灭魔法的边界必须与房间的墙壁重合,否则狡猾的敌人会躲在墙边,从而躲开此次攻击。小 A 只能发动一次该魔法,他希望魔法发动时能攻击到更多的敌人。小 A 选择寻求你的帮助,他告诉你了n个敌人的位置,你能告诉他,发动魔法最多能消灭多少个敌人吗?
例如:小 A 魔法的范围是 3*2,他共探查到了 5 个敌人,位置如下,他最多可以消灭 4 个敌人。
输入格式 第一行包含3个整数n, W, H(1 ≤ n ≤ 100, 1 ≤ W, H ≤ 1000)。代表共有n个敌人,魔法的打击范围是W∗H。
接下来n行,每行包含两个整数xi , yi (1 ≤ xi , yi ≤ 1000), 代表第i个敌人位于坐标(xi , yi )的房间。保证每个房间最多只有一个敌人。
输出格式 输出一个整数。代表小A发动魔法,最多消灭的敌人的数量。
输入样例1 5 3 2
输出样例1 4
输入样例2 5 2 3
输出样例2 3
题解 这个方法本质上依然是二维前缀和,但是只存储了一维的前缀和,每次遍历时重新计算二维前缀和。
为了节省运算资源,我们中间做了一个优化,就是裁剪掉没有人的区域,减少遍历范围,效果如图所示:
这个代码其实还有优化的余地,但是有些复杂就不写了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 int map[ 1001 ] [ 1001 ] ; int sumX[ 1001 ] [ 1001 ] ; int main ( ) { int n, w, h, x, y; scanf ( "%d %d %d" , & n, & w, & h) ; int startX = 1001 , startY = 1001 ; int maxX = 0 , maxY = 0 ; for ( int i = 0 ; i != n; ++ i) { scanf ( "%d %d" , & x, & y) ; [ y] [ x] = 1 ; if ( x < startX) startX = x; if ( y < startY) startY = y; if ( x > maxX) maxX = x; if ( y > maxY) maxY = y; } = min ( w, maxX - startX + 1 ) ; = min ( h, maxY - startY + 1 ) ; for ( x = startX; x <= maxX; ++ x) { for ( y = startY; y <= maxY; ++ y) { [ y] [ x] = sumX[ y] [ x - 1 ] + map[ y] [ x] ; } } int endX = max ( startX, maxX - w + 1 ) + 1 ; int endY = max ( startY, maxY - h + 1 ) + 1 ; int maxResult = min ( w * h, n) ; int result = 0 ; for ( x = startX; x != endX; ++ x) { for ( y = startY; y != endY; ++ y) { int temp = 0 ; for ( int k = 0 ; k != h; ++ k) { += sumX[ y + k] [ x + w - 1 ] - sumX[ y + k] [ x - 1 ] ; } if ( temp > result) { = temp; if ( result == maxResult) goto hear; } } } : printf ( "%d" , result) ; return 0 ; }
使用二维前缀和的方式计算结果,代码有优化的余地(即计算出遍历边界可以减少遍历数量)。
规定:左下角为坐标轴原点,右方向为X轴正轴,上方向为Y轴正轴。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 int sum[ 1001 ] [ 1001 ] ; bool input[ 1001 ] [ 1001 ] ; int get ( int leftX, int leftY, int width, int height) { int rightY = leftY + height - 1 ; int rightX = leftX + width - 1 ; return sum[ rightY] [ rightX] - sum[ leftY - 1 ] [ rightX] - sum[ rightY] [ leftX - 1 ] + sum[ leftY - 1 ] [ leftX - 1 ] ; } int main ( ) { int n, width, height, tempX, tempY; >> n >> width >> height; for ( int i = 0 ; i != n; ++ i) { scanf ( "%d %d" , & tempX, & tempY) ; [ tempY] [ tempX] = true ; } for ( int y = 1 ; y <= 1000 ; ++ y) { for ( int x = 1 ; x <= 1000 ; ++ x) { [ y] [ x] = sum[ y] [ x - 1 ] + sum[ y - 1 ] [ x] - sum[ y - 1 ] [ x - 1 ] ; if ( input[ y] [ x] ) ++ sum[ y] [ x] ; } } int result = 0 ; int endX = 1000 - width + 2 ; int endY = 1000 - height + 2 ; for ( int y = 1 ; y != endY; ++ y) { for ( int x = 1 ; x != endX; ++ x) { = max ( result, get ( x, y, width, height) ) ; } } << result; return 0 ; }
小A和小B历经千辛万苦,终于在一个洞穴中找到了宝藏。
在洞穴深处,他们发现了一颗价值连城的宝石,他们决定做一个游戏以决定宝石属于谁。
游戏规则如下:
每人在自己的回合必须选择其中一个操作:
拿走一块或者两块银子; 拿走一块金子。 无法继续进行操作的人被认为失败(即银子和金子都已经拿完)。
谁将得到宝石呢?
输入格式 多样例测试。
第一行输入T(T <= 100,000),代表样例数;
剩余T行,每行输入n, m(n < 1,000,000,000, m < 1,000,000,000) 代表银子和金子的数量。
输出格式 如果小A胜利,输出Alice,否则输出Bob。
输入样例 3
输出样例 Alice
题解 这道题是一道博弈题(听说还是小学奥数题 )。
我们先假设只有一堆金子或者一堆银子的情况。
首先我们先考虑金子那一堆,很显然,如果金子为偶数,那么先拿的人会输,否则先拿的人会赢。
接着我们再来看复杂一点的银子,如果有人玩过类似的游戏应该会很清楚,只要自己能够抢到一些特定的数就可以保证自己能够赢,下文中我们称这些数为“系列数”。我们很容易可以发现,只需要让自己拿到最后一个银子就能赢,那么如何保证自己能够拿到最后一个呢?只需要拿到倒数第四个就可以,因为假如我们拿到了倒数第四个,不论另一个人拿几个,我们都可以拿到最后一个。以此类推,可以发现我们只需要拿到1 4 7 10 ...一系列数字就可以了。
通过以上推算,我们很容易就可以判断假如自己先手能否抢到这一系列数字,很显然,当银子的数量不是3的倍数时我们就可以做到。
这时候我们再倒过来考虑一下,如果自己先手,有没有办法保证自己一定输?当然有,只要我们拿倒数第二个银子,就能保证对方拿最后一个,这样我们就一定会输。同理,我们可以知道,当我们拿到2 5 8 13 ...一系列数字时可以保证自己会输,那么很明显,如果我们先手并且银子的数量减一不是3的倍数时就可以了。
现在让我们回归题目,有两堆需要考虑,再让我们假设一个情况,就是两个人都先把其中一堆拿完,然后再拿另一堆。很明显,金子的结果是固定的,而银子相对而言却有周旋的空间,所以先手的人拿银子会更容易掌控局面。
那就让我们假设两个人都先拿银子。不难发现,如果想赢,我们还需要判断一下金子的数量。假如我们在金子堆先手的时候能够赢,那么我们应当让我们在银子堆输掉,这样才能保证我们先拿金子;如果我们在金子堆后手能赢,那么我们应当在银子堆胜利,这样才能让对方先拿金子。
有了这个思路就非常清晰了,很容易就能写出来下面的代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 int main ( ) { int t, n, m; scanf ( "%d" , & t) ; while ( t-- ) { scanf ( "%d %d" , & n, & m) ; if ( m % 2 == 0 ) { if ( n % 3 == 0 ) printf ( "Bob\n" ) ; else printf ( "Alice\n" ) ; } else { if ( ( n - 1 ) % 3 == 0 ) printf ( "Bob\n" ) ; else printf ( "Alice\n" ) ; } } return 0 ; }
现在我们再来考虑一下中间可能会有人去拿金子的情况,很显然,拿金子只能拿一个,并且下一次我们还能选择拿金子还是银子。所以我们不妨认为中间对方跑去拿金子只是改变了一下金子堆的总数,我们根据新的数量重新制定我们的计划就可以了。
现在的问题就变成了如果计划发生变化,我们能否保证自己依然能够拿到新的系列数?我们假设我们现在已经拿到了目前的系列数,比如是1 4 7 ...,当情况发生变化的时候我们应该拿到2 5 8 ...,很明显,这两个系列数的差值只有一,我们是可以从任意一个系列数中跳到另一个系列数中的。那么假如我们当前没有拿到系列数,比如现在的系列数为1 4 7 ...,新的系列数是2 5 8 ...,很明显,是有可能拿到新的系列数的
但是我们不要忘记这个游戏的两边是都想赢得,所以任意一方都不会走可能让自己输的一步的,如果我们能拿到系列数我们按照系列数走就一定能赢,如果拿不到系列数只要对方不给机会就永远都拿不到系列数。
综上所述,我们先前假设的先拿银子再拿金子的情况依然适用于两堆混合拿的情况,最终的代码我们就得出来了。
“欢迎来到靶场射击2.0.”
小A正在挑战一款叫做《靶场射击2.0》的游戏。游戏内共有两种靶子,一种是金色靶子,击中可以获得a积分,一种是普通靶子,击中可以获得b积分(a ≥ b)。每个靶子上都有一个字母,金色靶子上的为大写字母,普通靶子上的为小写字母。
当按下按键时,能得到所有对应字母相同的靶子的积分。如"WWWAAaa",按下键’A’,则能得到2∗a + 2∗b积分,按下键’W’,则能得到3∗a积分。
小A想挑战点不一样的,他想知道当前局面,按哪个键能得到的积分最多。
输入格式 第一行包含三个整数n, a, b(1 <= n <= 100000, 1 ≤ b ≤ a ≤ 10),代表n代表靶子数量,击中金色靶子获得的积分,击中普通靶子获得的积分。
第二行有n个字母,代表当前n个靶子上的字母。其中大写字母代表金色靶子,小写字母代表普通靶子。
输出格式 输出一个大写字符。代表小新按下该字符,能得到最多的积分。若有多个按键可以得到相同的积分,则输出字典序最小的那个字符。
输入样例1 7 3 2
输出样例1 A
输入样例2 7 5 2
输出样例2 W
题解
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 int main ( ) { int score[ 26 ] = { 0 } ; int n, a, b; char s; scanf ( "%d %d %d%*c" , & n, & a, & b) ; int maxScore = 0 ; while ( n-- ) { scanf ( "%c" , & s) ; if ( islower ( s) ) { [ s - 'a' ] += b; if ( score[ s - 'a' ] > maxScore) { = score[ s - 'a' ] ; } } else { [ s - 'A' ] += a; if ( score[ s - 'A' ] > maxScore) { = score[ s - 'A' ] ; } } } for ( int i = 0 ; i != 26 ; ++ i) { if ( score[ i] == maxScore) { printf ( "%c" , 'A' + i) ; break ; } } return 0 ; }
一个数通过最小次数交换数位变成20的倍数。问最少交换次数是多少?
输入格式 一个正整数T(1 <= T <= 10000),代表有T组输入。每个输入包含一个正整数N(1 <= N <= 1018 ),N没有前导0。
输出格式 最小的交换次数,每个占一行。如果不能交换出20的倍数,输出-1。
输入样例 2
输出样例 -1
题解 通过找规律可以发现,当一个数最后一个数是0,并且倒数第二个数是偶数时这个数一定是20的倍数。
这道题输入范围比较大,所以我们选择使用字符串来进行计算。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 int main ( ) { int n; scanf ( "%d" , & n) ; char str[ 20 ] ; while ( n-- ) { scanf ( "%s" , str) ; int startZero = - 1 , startOdd = - 1 ; int zero = 0 , odd = 0 ; int len = strlen ( str) ; for ( int i = len - 1 ; i != - 1 ; -- i) { int item = str[ i] - '0' ; if ( item == 0 ) { ++ zero; ++ odd; if ( startZero == - 1 ) startZero = i; else if ( startOdd == - 1 ) startOdd = i; } else if ( item % 2 == 0 ) { ++ odd; if ( startOdd == - 1 ) startOdd = i; } } if ( startZero == - 1 || startOdd == - 1 ) { printf ( "-1\n" ) ; continue ; } int end = len - 1 ; if ( startZero == end) { if ( startOdd == end - 1 ) printf ( "0\n" ) ; else printf ( "1\n" ) ; } else if ( startZero == end - 1 ) { if ( startOdd == end || zero != 1 ) printf ( "1\n" ) ; else printf ( "2\n" ) ; } else if ( ( str[ end - 1 ] - '0' ) % 2 == 0 ) { printf ( "1\n" ) ; } else printf ( "2\n" ) ; } return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 int main ( ) { int n; scanf ( "%d" , & n) ; ; while ( n-- ) { >> str; int startZero = - 1 , startOdd = - 1 ; int zero = 0 , odd = 0 ; for ( int i = str. length ( ) - 1 ; i != - 1 ; -- i) { int item = str[ i] - '0' ; if ( item == 0 ) { ++ zero; ++ odd; if ( startZero == - 1 ) startZero = i; else if ( startOdd == - 1 ) startOdd = i; } else if ( item % 2 == 0 ) { ++ odd; if ( startOdd == - 1 ) startOdd = i; } } if ( startZero == - 1 || startOdd == - 1 ) { printf ( "-1\n" ) ; continue ; } int end = str. length ( ) - 1 ; if ( startZero == end) { if ( startOdd == end - 1 ) printf ( "0\n" ) ; else printf ( "1\n" ) ; } else if ( startZero == end - 1 ) { if ( startOdd == end || zero != 1 ) printf ( "1\n" ) ; else printf ( "2\n" ) ; } else if ( ( str[ end - 1 ] - '0' ) % 2 == 0 ) { printf ( "1\n" ) ; } else printf ( "2\n" ) ; } return 0 ; }
学弟给了学长一份c语言代码,让学长帮忙debug,可是这段代码却是这样的:
1 2 # include <stdio.h> int main ( ) { int a, b; int c= a+ b; printf ( "Hello world!\n" ) ; return 0 ; }
这段代码机器能看懂,但是学长看不懂。 这代码有两个问题:没有换行缩进,二元运算符附近没有空格。 显然这是一段未格式化的代码,将其格式化成符合要求的格式。花括号不包含嵌套的情况。 格式要求:
分号后都需要换行 四个空格作为一个缩进单位 花括号{不换行,跟在前一个语句之后,但是隔开一个空格。 二元运算符周围需要放空格,因为学弟的代码只包含=,+,-,*,/,%这六个二元运算符 格式化后的代码:
1 2 3 4 5 6 7 # include <stdio.h> int main ( ) { int a, b; int c = a + b; printf ( "Hello world!\n" ) ; return 0 ; }
注意:代码中不包含多余的分号。代码中只调用printf函数,printf函数内不会出现花括号和二元运算符。
输入格式 两行可以编译的但是格式不符合的要求的代码,一行为头文件(保证只有一个头文件),一行为主函数代码。代码的问题如上所述,代码长度小于1000。代码中的花括号只包含主函数中的一对。保证代码主函数中有语句。
输出格式 满足格式格式要求的代码。
输入样例 #include<stdio.h>
输出样例 #include<stdio.h>
题解
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 int main ( ) { char str[ 1001 ] ; gets ( str) ; printf ( "%s\n" , str) ; gets ( str) ; = false; = false; = false; for ( int i = 0 ; i != str. length ( ) ; ++ i) { char item = str[ i] ; if ( inStr && item != '"' ) goto hear; switch ( item) { case '+' : case '-' : case '*' : case '/' : case '=' : case '%' : case '^' : if ( str[ i - 1 ] == ' ' ) { printf ( "%c " , item) ; } else { printf ( " %c " , item) ; } = true; break ; case ';' : printf ( "%c\n" , ';' ) ; = true; break ; case '&' : case '|' : if ( str[ i + 1 ] == item) { printf ( "%c%c " , item, item) ; ++ i; } else { printf ( " %c " , item) ; } = true; break ; case '{' : if ( space) printf ( "{\n" ) ; else printf ( " {\n" ) ; = true; break ; case '}' : printf ( "}" ) ; break ; case '!' : case '~' : if ( str[ i - 1 ] == ' ' ) printf ( "%c" , item) ; else printf ( " %c" , item) ; break ; case ' ' : if ( ! ( space || newLine) ) { printf ( " " ) ; = true; } break ; case '"' : = ! inStr; printf ( "\"" ) ; break ; default : : = false; if ( newLine) { = false; printf ( " " ) ; = true; } printf ( "%c" , item) ; break ; } } return 0 ; }
小H是一个考古学家,有一天他发现了海盗的宝藏,但是他只带了一个背包。现在摆在面前的宝物有100多件,每个宝物都有一个类型值(type)和一个珍贵程度(value)。现在要求选择若干个宝物(可以是0个)放进背包使得x * y最大,x为选择的不同type的数量,y为总的value值之和(同一种宝物value值一致,只计算一次value值)。
输入格式 第一行输入一个整数n表示物品的数量(1 ≤ n ≤ 200)。
第二行输入n个整数type_i表示每个物品的类型(1 ≤ type_i ≤ 200)。
第三行输入n个整数value_i(-100000 ≤ value_i ≤ 100000)。
输出格式 输出一个整数。
输入样例 2
输出样例 22
题解 这道题将输入按照value从大到小排序后,以贪心的思想就可以写出来了。注意:value为负值时不一定不取!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 typedef long long LL; struct node { = LLONG_MIN; = 0 ; bool operator < ( const node& obj) const { return value > obj. value; } } ; int main ( ) { int n, temp; scanf ( "%d" , & n) ; < node> key ( n) ; for ( auto & item : key) scanf ( "%lld" , & item. type) ; for ( auto & item : key) scanf ( "%lld" , & item. value) ; sort ( key. begin ( ) , key. end ( ) ) ; = 0 , y = 0 ; < LL> reType; for ( int i = 0 ; i != n; ++ i) { & item = key[ i] ; bool nonType = find ( reType. begin ( ) , reType. end ( ) , item. type) == reType. end ( ) ; = ( x + ( nonType ? 1 : 0 ) ) * ( y + item. value) ; if ( k > x * y) { if ( nonType) { ++ x; . push_back ( item. type) ; } if ( i == 0 || key[ i - 1 ] . value != item. value) { += item. value; } } } printf ( "%lld" , x * y) ; return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 typedef long long LL; struct node { = LLONG_MIN; = 0 ; < ( const node& obj) const { return value > obj. value; } } ; int compare ( const void * a, const void * b) { = ( ( node* ) b) -> value - ( ( node* ) a) -> value; if ( result < 0 ) return - 1 ; else if ( result > 0 ) return 1 ; return 0 ; } contain ( LL reType[ ] , int length, LL type) { for ( int i = 0 ; i != length; ++ i) { if ( reType[ i] == type) return true; } return false; } int main ( ) { int n, temp; scanf ( "%d" , & n) ; struct node key[ n] ; for ( int i = 0 ; i != n; ++ i) scanf ( "%lld" , & key[ i] . type) ; for ( int i = 0 ; i != n; ++ i) scanf ( "%lld" , & key[ i] . value) ; qsort ( key, n, sizeof ( node) , compare) ; = 0 , y = 0 ; [ n] ; int reLength = 0 ; memset ( reType, 0 , sizeof ( reType) ) ; for ( int i = 0 ; i != n; ++ i) { = contain ( reType, reLength, key[ i] . type) ; = ( x + ( hasType ? 0 : 1 ) ) * ( y + key[ i] . value) ; if ( k > x * y) { if ( ! hasType) { ++ x; [ reLength++ ] = key[ i] . type; } if ( i == 0 || key[ i - 1 ] . value != key[ i] . value) { += key[ i] . value; } } } printf ( "%lld" , x * y) ; return 0 ; }
#define int long long(OJ2788 ) 小A和队友一起比赛时,偷偷的加了一句"#define int long long"。导致队友wrong answer了三个小时。赛后被队友发现,小A的队友为了惩罚小A,决定让他抄2147483647遍"#define int long long"。绝望的小A希望你能帮他抄写10遍,你能帮帮他吗?
题解 1 2 3 4 5 int main ( ) { for ( int i = 0 ; i != 10 ; ++ i) printf ( "#define int long long\n" ) ; return 0 ; }
众所周知,小A学长是郑轻全能王,新来的学弟学妹们都特别崇拜小A学长,大家在每次比赛前都会摸一摸小A学长,为自己祈福。新生赛即将来临,n名同学为了能够获得更好的成绩,纷纷来找小A学长讨教算法并得到学长的祝福,小A学长为第i名学生辅导ai 分钟。小A学长有一项神奇的本领,为任意两名同学辅导的时间都不相同。小A学长会认为被辅导时间最长的同学将获得冠军,但是小A学长忙于辅导同学,没有时间计算谁会获得冠军,小A学长希望你帮他算一下。
输入格式 输入第一行包含一个整数n(1 <= n <= 5000),代表被小A学长辅导的同学的个数。接下来n行,每行包含一个字符串s(1 <= len(s) <= 20)和一个正整数(int范围内),分别代表学生的姓名和被辅导的时长。
输出格式 输出将会获得冠军的学生的姓名。
输入样例 4
输出样例 William
题解 通过swap减少数据的复制次数,同时简化代码。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 void swap ( char * * a, char * * b) { char * temp = * a; * a = * b; * b = temp; } int main ( ) { int n; scanf ( "%d" , & n) ; char * maxName = malloc ( 21 * sizeof ( char ) ) ; int maxTime = - 1 ; char * now = malloc ( 21 * sizeof ( char ) ) ; int nowTime; while ( n-- ) { scanf ( "%s %d" , now, & nowTime) ; if ( nowTime > maxTime) { swap ( & maxName, & now) ; = nowTime; } } printf ( "%s" , maxName) ; return 0 ; }
C语言中减少数据复制次数的优化在这里同样适用,不过数据量不大,并且直接复制数据写出来会更直观,所以这里就直接复制了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 int main ( ) { int n; scanf ( "%d" , & n) ; ; int maxTime = - 1 ; ; int nowTime; while ( n-- ) { >> now >> nowTime; if ( nowTime > maxTime) { = nowTime; = now; } } << maxName; return 0 ; }
小A终于来到了最后一题。小明翻找自己的背包,发现了很多能够提升自己能力值的药水。小A共发现了n种药水,第i种药水有ai 瓶,使用后能使能力值加bi 。但相同种类的药水,是不能连续使用的。小A觉得自己至少将能力值提升X(X >= 1),才有把握AK这场新生赛。药水的味道并不好,小明想尽量少的使用药水。你能告诉小A,他至少使用多少瓶药水, 才能使自己的能力提升至少X?
输入格式 第一行包含两个整数n, X(1 ≤ n ≤ 1000, 1 ≤ X ≤ 10,000,000,000,000,000);接下来n行,每行包括两个整数ai ,bi (1≤ai ,bi ≤10,000,000),代表第i种药水有ai 瓶,使用后能提示能力值bi 。
输出格式 如果小A不能使自己的能力提升至少X,输出-1;否则输出小A最少使用的药水的数量。
输入样例1 3 1000
输出样例1 -1
输入样例2 2 1000
输出样例2 9
题解 这道题我们使用二分法进行求解,设定一个值mid为当前取出的药水的数量,每次计算检查取出这个数量的药水能否达到X,可以的话就让mid向左移动,不可以的话就向右移动,直到确定最小可以达到X的mid。
很显然,求解前我们需要对药水按照增加的能力值进行排序,取得时候尽量取增加得能力值大的。我们排序时取一个巧,把数量为0的药水放到最后面,这样可以去掉一部分运算。
这道题最难的地方是如何确定取哪些药水,因为根据题意,我们不能连续拿同一种药水,假如输入数据为:
3 45
如果我们一味的先取最大的,就会导致最后一种药水只能取一个,使得计算结果错误。
我们不妨换一种思路,计算一下一种药水最多能够取多少。经过找规律,我们不难发现,假如我们要取mid瓶药水,当前还能够取now瓶药水,除去当前正在取得药水,其它药水总量为other,当前药水数量为amount,我们能取出当前药水的最大数量可以由下面这段代码计算:(LL是unsigned long long)
1 2 LL minA = min ( ( mid + 1 ) / 2 , other + 1 ) ; return min ( minA, min ( amount, now) ) ;
解释 对于(mid + 1) / 2,是根据mid - minA + 1 >= minA推出来的,即拿这个药水的数量不能超过要拿的药水的总量的一半,不然是不可能取出来的。
对于other + 1,是因为拿这个药水的数量也不能超过其它药水的总量+1,不然也是不可能取出来的。
min(amount, now)就很好理解了,这里不再解释。
根据上述内容,我们就能写出代码了:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 typedef unsigned long long LL; struct potion { ; ; bool operator < ( const potion& obj) const { if ( amount == 0 ) { return false ; } else if ( obj. amount == 0 ) { return true ; } return cap > obj. cap; } max ( LL mid, LL now, LL other) const { = min ( ( mid + 1 ) / 2 , other + 1 ) ; return min ( minA, min ( amount, now) ) ; } } ; int main ( ) { , x; = 0 ; scanf ( "%llu %llu" , & n, & x) ; < potion> list ( n) ; for ( auto & it : list) { scanf ( "%llu %llu" , & it. amount, & it. cap) ; += it. amount; } sort ( list. begin ( ) , list. end ( ) ) ; = sumAmount / 2 ; ; = sumAmount + 1 , left = 0 ; bool can = false ; do { = mid; = 0 ; for ( LL i = 0 ; i != n; ++ i) { = list[ i] . max ( mid, now, sumAmount - list[ i] . amount) ; -= take; += list[ i] . cap * take; } if ( sum == x) { = true ; break ; } if ( sum > x) { = true ; if ( right == mid) { = left; break ; } = mid; = ( left + mid) / 2 ; } else { if ( left == mid) { = right; break ; } = mid; = ( right - mid) / 2 + mid; } } while ( true ) ; if ( can) printf ( "%llu" , mid) ; else printf ( "-1" ) ; return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 typedef unsigned long long LL; struct potion { ; ; < ( const potion& obj) const { if ( amount == 0 ) { return false; } else if ( obj. amount == 0 ) { return true; } return cap > obj. cap; } } ; potionMax ( struct potion p, LL mid, LL now, LL other) { = min ( ( mid + 1 ) / 2 , other + 1 ) ; return min ( minA, min ( p. amount, now) ) ; } int compare ( const void * a, const void * b) { * ta = ( potion* ) a; * tt = ( potion* ) b; if ( ta-> amount == 0 ) return 1 ; if ( tt-> amount == 0 ) return - 1 ; = tt-> cap - ta-> cap; if ( dif > 0 ) return 1 ; if ( dif < 0 ) return - 1 ; return 0 ; } int main ( ) { , x; = 0 ; scanf ( "%llu %llu" , & n, & x) ; struct potion list[ n] ; for ( auto & it : list) { scanf ( "%llu %llu" , & it. amount, & it. cap) ; += it. amount; } qsort ( list, n, sizeof ( potion) , compare) ; = sumAmount / 2 ; ; = sumAmount + 1 , left = 0 ; = false; do { = mid; = 0 ; for ( LL i = 0 ; i != n; ++ i) { = potionMax ( list[ i] , mid, now, sumAmount - list[ i] . amount) ; -= take; += list[ i] . cap * take; } if ( sum == x) { = true; break ; } if ( sum > x) { = true; if ( right == mid) { = left; break ; } = mid; = ( left + mid) / 2 ; } else { if ( left == mid) { = right; break ; } = mid; = ( right - mid) / 2 + mid; } } while ( true) ; if ( can) printf ( "%llu" , mid) ; else printf ( "-1" ) ; return 0 ; }
创作不易,这次的题真的很难Orz,扫描下方打赏二维码支持一下吧ヾ(≧▽≦*)o
![]() 样我们判断是否是二进制的时候直接查表就可以了,不需要再计算。
样我们判断是否是二进制的时候直接查表就可以了,不需要再计算。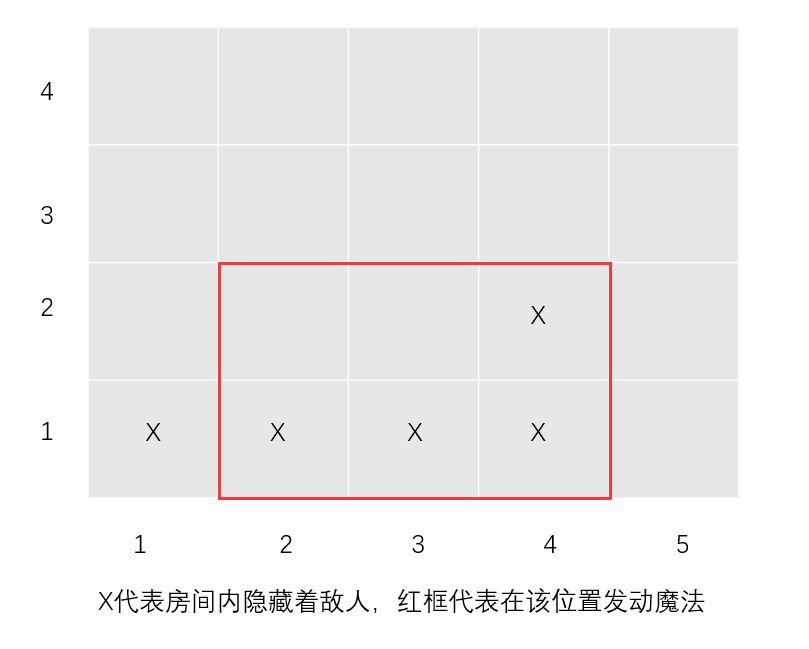

![]()





