注意 该博客是为了帮助同学学习,并非为了协助同学刷题,请读者保持自觉,请勿做CV工具人 。另外为了节省篇幅,代码中不再写明#include,如果遇到我没有声明的函数,那么就是某一个头文件中的函数,读者搜索“c + 函数名字”就能查到相关信息。
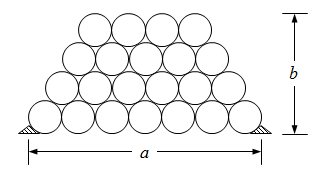
数油桶 题干 工人师傅将油桶码成如下图所示的梯形,数了数底层的油桶数和层数,就知道有多少油桶了。你知道他是怎么算的吗?
输入格式 底层油桶和层数
输出格式 油桶的数量
输入样例 7 4
输出样例 22
题解 很简单,不解释,直接上代码:
1 2 3 4 5 6 int main ( ) { int n, c; scanf ( "%d %d" , & n, & c) ; printf ( "%d" , ( 2 * n - c + 1 ) * c / 2 ) ; return 0 ; }
混合算数 题干 编程输出一个形如AXBXC的四则运算式的结果。例如:1+23、5 6+7、100-50/5。
输入格式 在一行内包含一个算式。算式中有2个运算符,3个操作数。运算符保证是“+、-、*、/”之一,所有的操作数都是非负整数。除法运算结果与C语言整数除法规则一致,所有测试数据中保证除数不为0。
输出格式 输出算式结果。
输入样例 1+2*3
输出样例 7
题解 这道题有一个点需要我们注意,即“除法运算结果与C语言整数除法规则一致”。这时候我们思考一下,C语言的整数除法规则是什么?是向下取整,比如1 / 2 = 0、3 / 2 = 1。
然后我们便需要考虑运算顺序的问题,运算时我们应当先计算乘除法再计算加减法。一个比较简单的实现方法是如果第二个运算符是乘除就先计算后面的运算再计算前面的运算。但是这个方法有一个非常显著的缺陷,比如:3*1/2,如果先计算1/2整体答案就会变成0,但是最终答案应该为1。
所以我们还是应当先判断第一个运算符再判断第二个运算符。这时候易得,当第一个运算符为乘除时一定优先计算前面的运算,当第一个运算符并且第二个运算符是乘除时应当优先计算后面的运算。
由此,我们可得如下代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 # include <stdlib.h> void task ( char op, int a, long long * result) { switch ( op) { case '+' : * result += a; break ; case '-' : * result = a - * result; break ; } } int main ( ) { int a, b, c; char op0, op1; scanf ( "%d%c%d%c%d" , & a, & op0, & b, & op1, & c) ; long long result; if ( ( op0 == '+' || op0 == '-' ) && ( op1 == '*' || op1 == '/' ) ) { switch ( op1) { case '*' : = ( long long ) b * c; task ( op0, a, & result) ; break ; case '/' : = ( long long ) b / c; task ( op0, a, & result) ; break ; } } else { switch ( op0) { case '*' : result = ( long long ) a * b; break ; case '/' : result = ( long long ) a / b; break ; case '+' : result = ( long long ) a + b; break ; case '-' : result = ( long long ) a - b; break ; } switch ( op1) { case '+' : result += c; break ; case '-' : result -= c; break ; case '*' : result *= c; break ; case '/' : result /= c; break ; } } printf ( "%lld" , result) ; return 0 ; }
小H的思维题 题干 先来一题思维题,给你四个整数,a、b、x、y。一开始,a≥x和b≥y。您可以执行以下操作不超过n次。
选择其中之一a或b把它减少一。但是,a不能比x小,b不能比y小。 你的任务是通过不超过n次操作后,最小化a∗b。
你得回答t次独立的case。
输入格式 输入的第一行包含一个整数。t (1≥t≥2∗104 )测试用例的数量。然后接下来是t个测试用例。
测试用例的唯一行包含五个整数。a、b、x、y和n(1≤a,b,x,y,n≤109 )。对输入的附加限制:a≥x和b≥y一直都是。
输出格式 对每个测试用例,打印一个整数:通过不超过n次操作后,最小化a∗b。
输入样例 7
输出样例 70
样例解释 在示例的第一个测试用例中,需要减少b三次10*7=70。
在示例的第二个测试用例中,需要减少a有一次,b一次并获得11*7=77。
在示例的第六个测试用例中,需要减少a五次5*11=55。
在示例的第七个测试用例中,需要减少b十次10*1=10。
题解 我们来列出一些情况分类讨论:
a = 100, b = 100, x = 1, y = 1, n = 5a、b中任意一个数减5就可以得到答案。 a = 50, b = 100, x = 45, y = 45, n = 10a减到45,将b减到95;在第三个情况中,我们不应该对任何一个数进行减法。 a = 50, b = 50, x = 50, y = 50, n = 10a还是b?我们可以试一下,如果先减b,最终的结果是40*40=1600,如果先减a,最终的结果是35*45=1400,显而易见,我们应该先减a。 a = 50, b = 45, x = 35, y = 40, n = 15 a = 50, b = 50, x = 1, y = 1, n = 0 根据以上信息我们总结一下,进行运算时,我们应当尽量地减出一个最小的数字(注意不是把当前最小的数字减到其能达到的最小)。同时通过例题我们也可以看到,中间出现了非常大的数字,所以只用int绝对会导致数据溢出,这里我们就用long long来保证数据正常(如果连long long都存不下只能用大数字了,但是我们这个水平的竞赛题中如果不单独考大数字是绝对不会涉及到大数字的)。
所以我们可以得到如下代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 int main ( ) { int t; int a, b, x, y, n; scanf ( "%d" , & t) ; while ( t-- ) { scanf ( "%d %d %d %d %d" , & a, & b, & x, & y, & n) ; int xMin = a - min ( a - x, n) ; int yMin = b - min ( b - y, n) ; if ( xMin < yMin) { -= ( a - xMin) ; = xMin; if ( n != 0 ) b -= min ( b - y, n) ; } else { -= ( b - yMin) ; = yMin; if ( n != 0 ) a -= min ( a - x, n) ; } printf ( "%lld\n" , ( long long ) a * b) ; } return 0 ; }
字符串A-B 题干 本题要求你计算A-B。不过麻烦的是,A和B都是字符串 —— 即从字符串A中把字符串B所包含的字符全删掉,剩下的字符组成的就是字符串A-B。
输入格式 输入在2行中先后给出字符串A和B。每个字符串都是由可见的ASCII码组成,最后以换行符结束。
输出格式 在一行中打印出A-B的结果字符串。
输入样例: I love Python! It’s a fun game!
输出样例: I lv Pythn! It’s fn gm!
题解 这道题有些人可能会想复杂,即先删除字符串内容再打印字符串,实际上我们只需要一个字符一个字符打印,在打印的过程中处理字符串就行了。
有了思路就很容易写出代码了:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 int main ( ) { char source[ 1001 ] , del[ 1001 ] ; gets ( source) ; gets ( del) ; int sLen = strlen ( source) ; int dLen = strlen ( del) ; for ( int i = 0 ; i != sLen; ++ i) { = false; for ( int k = 0 ; k != dLen; ++ k) { if ( del[ k] == source[ i] ) { = true; break ; } } if ( isFind) continue ; printf ( "%c" , source[ i] ) ; } return 0 ; }
魔镜 题干 传说魔镜可以把任何接触镜面的东西变成原来的两倍,不过增加的那部分是反的。例如,对于字符串XY,若把Y端接触镜面,则魔镜会把这个字符串变为XYYX;若再用X端接触镜面,则会变成XYYXXYYX。对于一个最终得到的字符串(可能未接触魔镜),请输出没使用魔镜之前,该字符串最初可能的最小长度。
输入格式 测试数据有多组,处理到文件尾。每组测试输入一个字符串(长度小于100,且由大写英文字母构成)。
输出格式 对于每组测试数据,在一行上输出一个整数,表示没使用魔镜前,最初字符串可能的最小长度。
输入样例 XYYXXYYX
输出样例 2
题解 这道题说的很复杂,实际上就是判断是否为对称字符串。我们来考虑一下对称字符串需要满足什么条件。
到这里,思路应该就很清晰了,我们给出代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 int main ( ) { char str[ 101 ] ; while ( gets ( str) ) { int len = strlen ( str) ; while ( true) { if ( len % 2 != 0 ) break ; for ( int i = 0 , j = len - 1 ; i < j; ++ i, -- j) { if ( str[ i] != str[ j] ) { goto hear; } } /= 2 ; } : printf ( "%d\n" , len) ; } return 0 ; }
求n以内最大的k个素数以及它们的和 题干 本题要求计算并输出不超过n的最大的k个素数以及它们的和。
输入格式 输入在一行中给出n(10≤n≤10000)和k(1≤k≤10)的值。
输出格式 在一行中按下列格式输出:素数1 + 素数2 + … + 素数k = 总和值
其中素数按递减顺序输出,若n以内不够k个素数,则按实际个数输出。
输入样例1 1000 10
输出样例1 997+991+983+977+971+967+953+947+941+937=9664
输入样例2 12 6
输出样例2 11+7+5+3+2=28
题解 很简单,不解释,上代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 int main ( ) { int n, k; scanf ( "%d %d" , & n, & k) ; = false; unsigned long long result = 0 ; for ( int i = n; i != 1 && k != 0 ; -- i) { if ( isSu ( i) ) { if ( start) printf ( "+" ) ; printf ( "%d" , i) ; += i; = true; -- k; } } printf ( "=%llu" , result) ; return 0 ; }
判断上三角矩阵 题干 上三角矩阵指主对角线以下的元素都为0的矩阵;主对角线为从矩阵的左上角至右下角的连线。
本题要求编写程序,判断一个给定的方阵是否上三角矩阵。
输入格式 输入第一行给出一个正整数T,为待测矩阵的个数。接下来给出T个矩阵的信息:每个矩阵信息的第一行给出一个不超过10的正整数n。随后n行,每行给出n个整数,其间以空格分隔。
输出格式 每个矩阵的判断结果占一行。如果输入的矩阵是上三角矩阵,输出“YES”,否则输出“NO”。
输入样例 3
输出样例 YES
题解 这道题也很简单,不过很多人可能会选择将输入的矩阵存储起来,实际上我们不需要存储矩阵的内容。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 int main ( ) { int t, n, temp; scanf ( "%d" , & t) ; while ( t-- ) { scanf ( "%d" , & n) ; = true; for ( int y = 0 ; y != n; ++ y) { for ( int x = 0 ; x != n; ++ x) { scanf ( "%d" , & temp) ; if ( result && x < y && temp != 0 ) result = false; } } printf ( result ? "YES\n" : "NO\n" ) ; } return 0 ; }
一元多项式的乘法与加法运算 题干 设计函数分别求两个一元多项式的乘积与和。
输入格式 输入分2行,每行分别先给出多项式非零项的个数,再以指数递降方式输入一个多项式非零项系数和指数(绝对值均为不超过1000的整数)。数字间以空格分隔。
输出格式 输出分2行,分别以指数递降方式输出乘积多项式以及和多项式非零项的系数和指数。数字间以空格分隔,但结尾不能有多余空格。零多项式应输出0 0。
输入样例 4 3 4 -5 2 6 1 -2 0
输出样例 15 24 -25 22 30 21 -10 20 -21 8 35 6 -33 5 14 4 -15 3 18 2 -6 1
题解 这道题用到了很多的数组,所以我们使用c++来写,想要c的解法可以参考这篇博客 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 # include <bits/stdc++.h> using std:: string; using std:: vector; struct node { long long a; long long e; operator * ( const node& obj) const { return { a * obj. a, e + obj. e} ; } & operator += ( const node& obj) { += obj. a; return * this ; } bool operator < ( const node& obj) const { return e > obj. e; } } ; int main ( ) { < node> arg[ 2 ] ; int n, a, e; for ( int i = 0 ; i != 2 ; ++ i) { scanf ( "%d" , & n) ; while ( n-- ) { scanf ( "%d%d" , & a, & e) ; [ i] . push_back ( { a, e} ) ; } } < node> c; for ( const auto & node0 : arg[ 0 ] ) { for ( const auto & node1 : arg[ 1 ] ) { = node0 * node1; for ( auto & item : c) { if ( item. e == temp. e) { += temp; goto hear; } } . push_back ( temp) ; : ; } } < int > j; bool * isAdd = new bool [ arg[ 1 ] . size ( ) ] ; for ( int i = 0 ; i != arg[ 0 ] . size ( ) ; ++ i) { = arg[ 0 ] [ i] ; for ( int l = 0 ; l != arg[ 1 ] . size ( ) ; ++ l) { if ( arg[ 1 ] [ l] . e == result. e) { += arg[ 1 ] [ l] ; [ l] = true ; } } . push_back ( result) ; } for ( int i = 0 ; i != arg[ 1 ] . size ( ) ; ++ i) { if ( ! isAdd[ i] ) j. push_back ( arg[ 1 ] [ i] ) ; } :: sort ( c. begin ( ) , c. end ( ) ) ; :: sort ( j. begin ( ) , j. end ( ) ) ; bool start = false ; for ( const auto & item : c) { if ( item. a == 0 ) continue ; if ( start) printf ( " " ) ; printf ( "%lld %lld" , item. a, item. e) ; = true ; } if ( ! start) printf ( "0 0" ) ; printf ( "\n" ) ; = false ; for ( const auto & item : j) { if ( item. a == 0 ) continue ; if ( start) printf ( " " ) ; printf ( "%lld %lld" , item. a, item. e) ; = true ; } if ( ! start) printf ( "0 0" ) ; return 0 ; }
石子合并 题干 在一个圆形操场的四周摆放 N 堆石子,现要将石子有次序地合并成一堆.规定每次只能选相邻的 2 堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。
试设计出一个算法,计算出将 N 堆石子合并成 1 堆的最小得分和最大得分。
输入格式 数据的第 1 行是正整数N,表示有N堆石子。第 2 行有N个整数,第i个整数 ai 表示第i堆石子的个数。
输出格式 输出共 2 行,第 1 行为最小得分,第 2 行为最大得分。
输入样例 4
输出样例 43
题解 这道题用的是区间DP,网上搜“环形石子合并”能搜到很多题解,想学习的同学可以先学习动态规划思想,然后学习“直线型石子合并”,最后再学习本道例题。
网上的“环形石子合并”大多选择将数据复制一遍来模拟环形,这里我选择了另一种方法,巧妙地利用了数组中的空余空间,节省了内存。题太难,不解释,直接上代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 # include <bits/stdc++.h> int n; int costIndex ( int index) { return index < n ? index : index - n; } struct array { public : explicit array ( int init) { memset ( value, init, sizeof ( value) ) ; } int & at ( int start, int end) { return value[ costIndex ( start) ] [ costIndex ( end) ] ; } private : int value[ 300 ] [ 300 ] = { } ; } ; minResult ( 0b01111111 ) ; maxResult ( 0 ) ; sum ( 0 ) ; int stone[ 300 ] ; int main ( ) { int temp; scanf ( "%d" , & n) ; for ( int i = 0 ; i != n; ++ i) { scanf ( "%d" , & stone[ i] ) ; . at ( i, i) = 0 ; . at ( i, i) = stone[ i] ; } for ( int start = 0 ; start != n; ++ start) { for ( int len = 1 ; len != n; ++ len) { . at ( start, len + start) = . at ( start, len + start - 1 ) + stone[ costIndex ( len + start) ] ; } } for ( int len = 1 ; len != n; ++ len) { for ( int start = 0 ; start != n; ++ start) { int end = start + len; for ( int k = start; k != end; ++ k) { . at ( start, end) = std:: min ( minResult. at ( start, end) , . at ( start, k) + minResult. at ( k + 1 , end) + sum. at ( start, end) ) ; . at ( start, end) = std:: max ( maxResult. at ( start, end) , . at ( start, k) + maxResult. at ( k + 1 , end) + sum. at ( start, end) ) ; } } } int min = INT_MAX, max = INT_MIN; for ( int i = 0 ; i != n; ++ i) { int minValue = minResult. at ( i, i + n - 1 ) ; int maxValue = maxResult. at ( i, i + n - 1 ) ; if ( min > minValue) min = minValue; if ( max < maxValue) max = maxValue; } printf ( "%d\n%d" , min, max) ; return 0 ; }
创作不易,扫描下方打赏二维码支持一下吧ヾ(≧▽≦*)o
结尾无空行
结尾无空行
结尾无空行
结尾无空行
结尾无空行
结尾无空行
结尾无空行
结尾无空行
结尾无空行